Objective Functions¶
-
class
macaw.objective_functions.L1Norm(y, model)[source]¶ Defines the L1 Norm loss function. L1 norm is usually useful to optimize the “median” model, i.e., it is more robust to outliers than the quadratic loss function.
\[\arg \min_{\theta \in \Theta} \sum_k |y_k - f(x_k, \theta)|\]Examples
>>> from macaw.objective_functions import L1Norm >>> from macaw.optimizers import MajorizationMinimization >>> from macaw.models import LinearModel >>> import numpy as np >>> # generate fake data >>> np.random.seed(0) >>> x = np.linspace(0, 10, 200) >>> fake_data = x * 3 + 10 + np.random.normal(scale=2, size=x.shape) >>> # build the model >>> my_line = LinearModel(x) >>> # build the objective function >>> l1norm = L1Norm(fake_data, my_line) >>> # perform optimization >>> mm = MajorizationMinimization(l1norm) >>> mm.compute(x0=(1., 1.)) >>> # get best fit parameters >>> print(mm.x) [ 2.96016173 10.30580954]
Attributes
y (array-like) Observed data model (callable) A functional form that defines the model Methods
__call__(theta)Calls evaluate()evaluate(theta)fit(x0[, n, xtol, ftol])gradient_surrogate(theta, theta_n)Computes the gradient of the surrogate function. surrogate_fun(theta, theta_n)Evaluates a surrogate function that majorizes the L1Norm.
-
class
macaw.objective_functions.L2Norm(y, model, yerr=1)[source]¶ Defines the squared L2 norm loss function. L2 norm tends to fit the model to the mean trend of the data.
\[\arg \min_{w \in \mathcal{W}} \frac{1}{2}||y - f(X, \mathbf{w})||^{2}_{2}\]Examples
>>> import numpy as np >>> from macaw.objective_functions import L2Norm >>> from macaw.optimizers import GradientDescent >>> from macaw.models import LinearModel >>> # generate fake data >>> np.random.seed(0) >>> x = np.linspace(0, 10, 200) >>> fake_data = x * 3 + 10 + np.random.normal(scale=2, size=x.shape) >>> # build the model >>> my_line = LinearModel(x) >>> # build the objective function >>> l2norm = L2Norm(fake_data, my_line) >>> # perform optimization >>> gd = GradientDescent(l2norm.evaluate, l2norm.gradient) >>> gd.compute(x0=(1., 1.)) >>> # get the best fit parameters >>> print(gd.x) [ 2.96263148 10.32861519]
Attributes
y (array-like) Observed data model (callable) A functional form that defines the model yerr (scalar or array-like) Weights or uncertainties on each observed data point Methods
__call__(theta)Calls evaluate()evaluate(theta)fit(x0[, optimizer, n, xtol, ftol])gradient(theta)
-
class
macaw.objective_functions.BernoulliLikelihood(y, model)[source]¶ Implements the negative log likelihood function for independent (possibly non-identical distributed) Bernoulli random variables. This class also contains a method to compute maximum likelihood estimators for the probability of a success.
More precisely, the MLE is computed as
\[\arg \min_{\theta \in \Theta} - \sum_{i=1}^{n} y_i\log\pi_i(\mathbf{\theta}) + (1 - y_i)\log(1 - \pi_i(\mathbf{\theta}))\]Examples
>>> import numpy as np >>> from macaw import BernoulliLikelihood >>> from macaw.models import ConstantModel as constant >>> # generate integer fake data in the set {0, 1} >>> np.random.seed(0) >>> y = np.random.choice([0, 1], size=100) >>> # create a model >>> p = constant() >>> # perform optimization >>> ber = BernoulliLikelihood(y=y, model=p) >>> result = ber.fit(x0=[0.3]) >>> # get best fit parameters >>> print(result.x) [ 0.55999999] >>> print(np.mean(y>0)) # theorectical MLE 0.56 >>> # get uncertainties on the best fit parameters >>> print(ber.uncertainties(result.x)) [ 0.04963869] >>> # theorectical uncertainty >>> print(np.sqrt(.56 * .44 / 100)) 0.049638694584
Attributes
y (array-like) Observed data model (callable) A functional form that defines the model for the probability of success Methods
__call__(theta)Calls evaluate()evaluate(theta)fisher_information_matrix(theta)fit(x0[, optimizer, n, xtol, ftol])gradient(theta)uncertainties(theta)
-
class
macaw.objective_functions.Lasso(y, X, alpha=1)[source]¶ Implements the Lasso objective function.
Lasso is usually used to estimate sparse coefficients.
\[\arg \min_{w \in \mathcal{W}} \frac{1}{2\cdot n_{\text{samples}}}||y - X\mathbf{w}||^{2}_{2} + \alpha||\mathbf{w}||^{1}_{1}\]Methods
__call__(theta)Calls evaluate()evaluate(theta)fit(x0[, n, xtol, ftol])gradient_surrogate(theta, theta_n)surrogate_fun(theta, theta_n)
-
class
macaw.objective_functions.RidgeRegression(y, X, alpha=1)[source]¶ Implements Ridge regression objective function.
Ridge regression is a specific case of regression in which the model is linear, the objective function is the L2 norm, and the regularization term is the L2 norm.
\[\arg \min_{w \in \mathcal{W}} \frac{1}{2}||y - X\mathbf{w}||^{2}_{2} + \alpha||\mathbf{w}||^{2}_{2}\]Methods
__call__(theta)Calls evaluate()evaluate(theta)fit(x0[, optimizer, n, xtol, ftol])gradient(theta)
-
class
macaw.objective_functions.LogisticRegression(y, X)[source]¶ Implements a Logistic regression objective function for Binary classification.
Methods
__call__(theta)Calls evaluate()evaluate(theta)fisher_information_matrix(theta)fit(x0[, optimizer, n, xtol, ftol])gradient(theta)gradient_surrogate(theta, theta_n)predict(X)surrogate_fun(theta, theta_n)uncertainties(theta)
-
class
macaw.objective_functions.L1LogisticRegression(y, X, alpha=0.1)[source]¶ Implements a Logistic regression objective function with L1-norm regularization for Binary classification.
Methods
__call__(theta)Calls evaluate()evaluate(theta)fit(x0[, n, xtol, ftol])gradient_surrogate(theta, theta_n)predict(X)surrogate_fun(theta, theta_n)
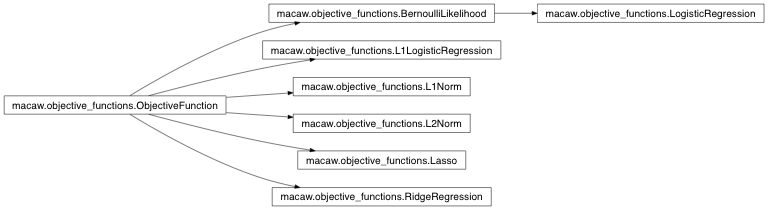
Inheritance Diagram¶